The Relationship Between Compound Interest and Time

4 min read

Recently Paula Pant interviewed Suze Orman on the Afford Anything Podcast. One point that Suze kept emphasizing was that she thought it was a bad idea for most people to quit their jobs when they’re young (even if they are financially independent) because they’ll lose an income stream and thus they’ll miss out on the power of compound interest over the course of several decades.

Here’s an excerpt from the interview:

Suze: “Here’s the real problem. If you’ve achieved financial independence, and you’re no longer putting money into your retirement accounts, you are losing the compounding years of your life. And what do I mean by that? When you’re younger, and you lose this as you get older, you put $100 a month into a Roth IRA. Put it into a Good Standard and Poor’s 500 index fund, and you do so every single month until you are 65, for 40 years. Now you’ll have a million dollars with a 12 percent annual average rate of return.

But if you wait until you’re 35 to start and you put in $100 every month…at 65, you’d have only $300,000. Those 10 years costs you $700,000. So when you are younger, your money that you invest makes money. And that money makes money, and that money makes money, and your money compounds and you cannot make up for that with sums of money later on in life.

So when you stop working early, and you’re now not able to continue to contribute because you’re not having an income coming in, now you’re financially independent, you’ve retired. So now you’re living off of the money that you have, if you want to be. How do you take advantage of your compounding years?”

Suze gives the example of someone who contributes $100 per month into a retirement account for 40 years at a 12% rate of return. Setting aside the fact that a 12% annual rate of return after inflation is a lofty assumption, let’s visualize exactly what Suze is saying.

For simplicity, I’ll use $1,200 per year as the annual investment. Here’s how a $1,200 annual investment would grow over 40 years at a 12% rate of return:

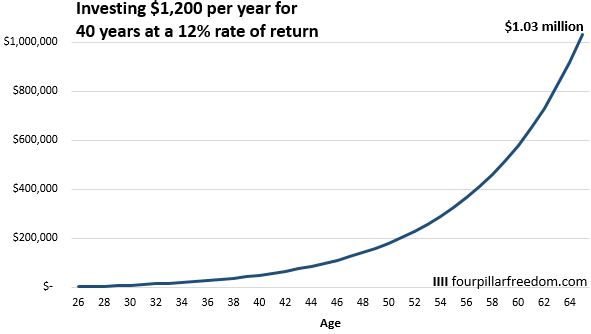
Suze’s math checks out on this one. Someone who invests $1,200 per year for 40 years at a 12% rate of return would indeed end up with about a million bucks.

And here’s a look at someone who delays investing for 10 years. This person also invests $1,200 per year at a 12% rate of return, but they only invest for 30 total years:

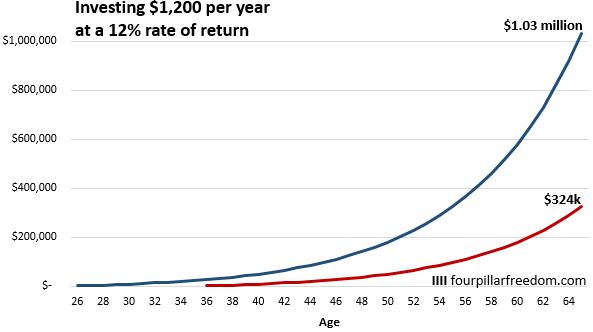
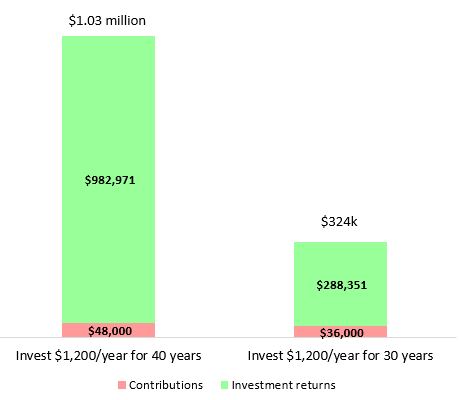
Again Suze’s math checks out. Someone who delays investing for 10 years would only end up with $324k. As she says, the difference between the two ending amounts is about $700k.

And Suze is also correct that missing out on ten years of compounding makes a huge difference:

But let’s go back to this remark by Suze:

“So when you stop working early, and you’re now not able to continue to contribute because you’re not having an income coming in…How do you take advantage of your compounding years?”

Here she is making the assumption that compound interest has to play an important role in wealth-building. But in reality, if your savings rate is high enough, your path to financial independence is shortened, and compound interest doesn’t actually matter as much.

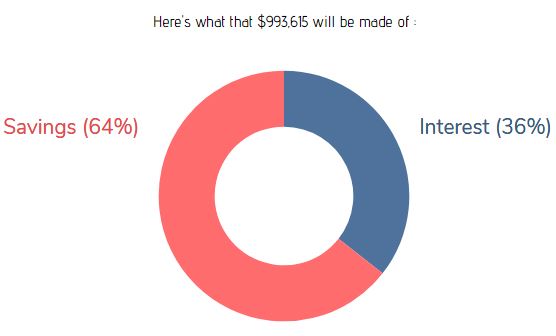
Consider a couple who aims to save $1 million before quitting their jobs. If they earn a combined $80k per year after taxes and are able to save and invest $40k per year, they’ll be able to save almost $1 million in about 16 years assuming a 5% annual rate of return (courtesy of the savings vs. investment return calculator):

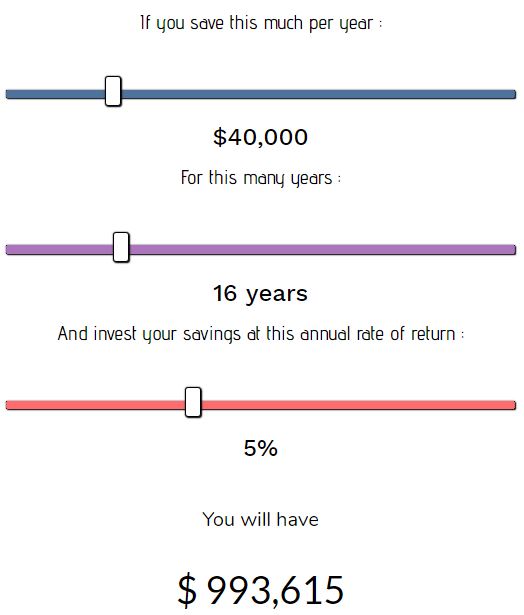
And a whopping 64% of this total net worth would come from savings alone:

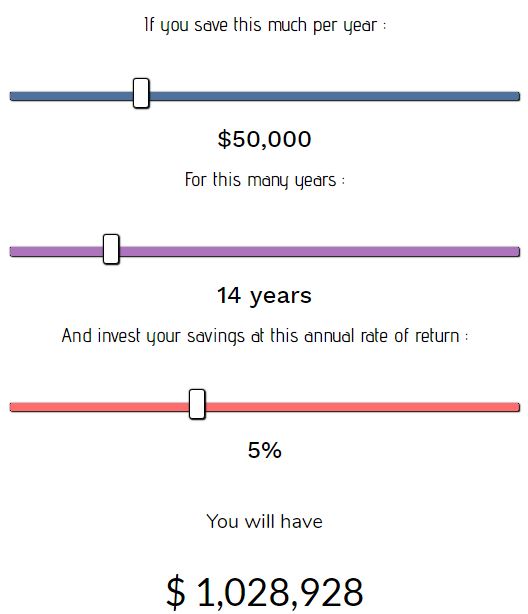
If this same couple was able to save $50k per year instead, they would be able to accumulate over $1 million in only 14 years:

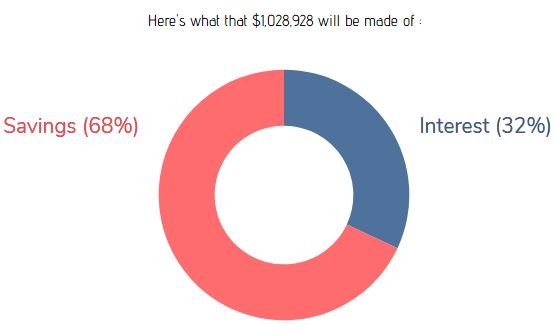
And 68% of this would come from savings alone:

As illustrated by the financial independence grid, the higher your savings rate, the shorter your path to financial independence:

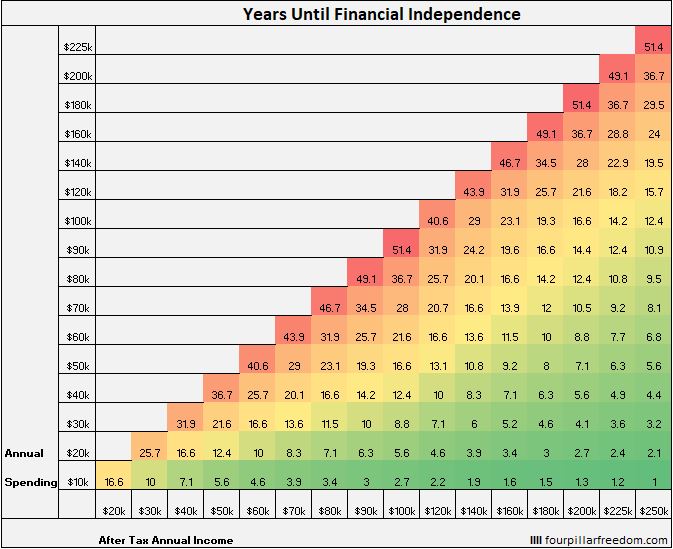
And the shorter your path to financial independence, the less compound interest plays a role in building your net worth.

The answer to Suze’s question: “If you stop working early, how do you take advantage of your compounding years?” is that you don’t take advantage of your compounding years because you don’t need to. With a high enough savings rate, you don’t need to rely on compound interest to fuel your net worth growth. 

If your goal is to grow your net worth from $0 to $1 million, who cares what percentage of that growth comes from compound interest? In particular, if you aspire to achieve F.I. in 15 years or less, the amount you save each year matters more than the investment returns you earn.

Listen to the entire Suze Orman interview here as well as Paula’s response episode here.

Full Disclosure: Nothing on this site should ever be considered to be advice, research or an invitation to buy or sell any securities, please see my Terms & Conditions page for a full disclaimer.